The Justified Ancients of Mu Mu. Dan’s MEGA65 Digest for March 2024.

[Did you know: All issues of the Digest have an audio version! Search for “Dan’s MEGA65 Digest” in your favorite podcast app, or check out the audio player at the top of each issue. — Dan]

There are two methods for making sound and music with the MEGA65, as it is currently implemented. The first method is the four SID chips, programmable devices that generate waveforms with requested parameters using analog electronic components. We took a dive into the SID chips back in—November 2022?? How long have I been doing this?? …

The MEGA65 can produce sound another way. Pulse-Code Modulation (PCM) describes a waveform as a sequence of values over time, literally the shape of the desired waveform as a series of high and low numbers, as if drawn on a graph. The computer feeds these numbers into a device called a Digital-Analog Converter (DAC) that produces the waveform in that shape, as if rapidly changing the position of a speaker membrane according to each value. The MEGA65 has four DACs, and these waveforms are mixed with the rest of the audio system to produce the stereo audio output of the computer.

With PCM, a computer can reproduce real-world sounds captured by a microphone, such as human speech or musical instruments. Today, we take this extremely for granted: modern computers generate pretty much all sound using PCM waveforms. We used to call this “digitized sound,” in contrast with “synthesized sound.” Now we just call it “sound.” While PCM gives a computer program much more control over the generated sound, the trade-off is memory: relative to the memory sizes of 1980’s computers, PCM sound data takes a huge amount of space, depending on the length and quality of the sounds.

In this issue, we’ll look at how to control the MEGA65’s DACs to play digitized sound, as well as techniques for wrangling sound data for use in your programs. As usual, we’ll spend a bit too much time nerding out on theory and file formats.

Are you ready? Here we go.

MEGA65 News

Featured Files

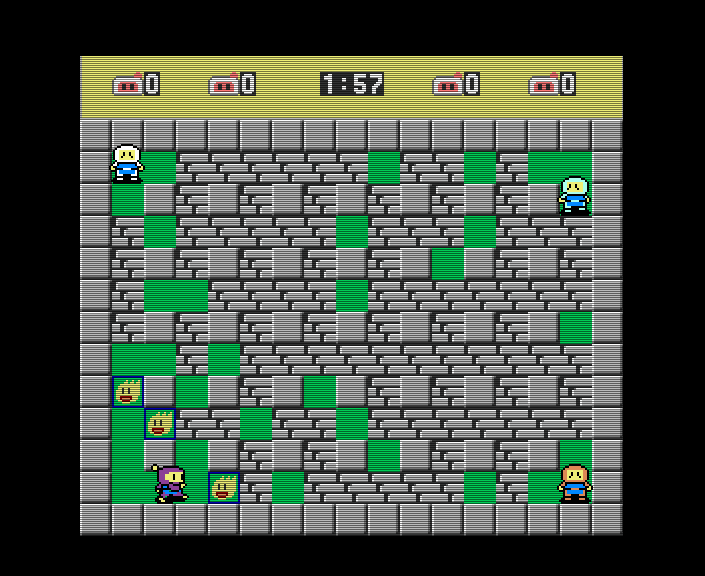
Bomb’em All by btoschi, an explosive action game for two to four players. Drop bombs, pick up items, and break through walls while trying to trap your opponents in the blast zone. The game supports the Four Fun joystick adapter for four joysticks, or can be played with a mix of joystick and keyboard controls.

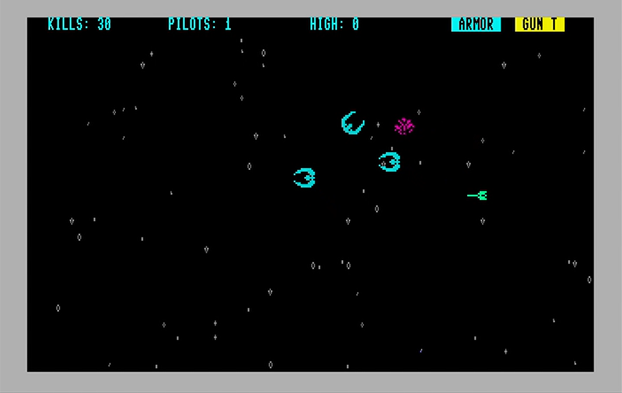
BASIC Star Galactica by jim_64, a space battle adventure. Destroy the Cylons and protect the fleet—and the future of humanity. Don’t miss the downloadable, printable disk label and manual.

fredrikr has prepared the fourth in his series of text adventure game bundles for the MEGA65, featuring modern classics from the interactive fiction community. This pack includes a variety of games released from 1995 to 2023, all playable on the MEGA65 thanks to the Ozmoo Z-machine player. (See the Digest from October 2022 for more on Ozmoo and MEGA65 adventure gaming.)

Another arcade core from muse! In Ghosts’n Goblins (1985), you are brave knight Sir Arthur, on a quest to save the Princess Prin-Prin. Don your armor—and take care not to lose it—while fighting waves of zombies, giants, demons, and other monsters. This classic from Capcom is considered one of the best video games of all time—and one of the most difficult. As with the other arcade cores, you will need to find the game ROM online, and follow the instructions to install it.

In Stranded, a graphical adventure game by Magnus Heidenborn, your boat has crashed and washed ashore a deserted island. Magnus wrote Stranded for the Commodore 64, specifically the modern TheC64 clone. Gurce ported it to the MEGA65, and added original music. I especially appreciate the novel keyboard-based linear travel and exploration mechanic, which works around common issues with point-and-click adventure games. Check it out!

Expansion board progress

Paul is making progress on the MEGA65 expansion board project. As we reviewed in a previous issue, this project intends to produce an internal hardware expansion that adds component video output, a Commodore user port, a tape port, and a port for the never-released 1565 external floppy drive that was originally intended for the Commodore 65. The goal is for these expansion boards to be made entirely out of printed circuit boards (PCBs) and common components with open source designs, so anyone can order and assemble one from any PCB fabricator.

The latest prototype includes a way to connect an ESP32 wireless Internet module (!), and routes a path for the optional JTAG adapter to a firmly mounted microUSB port accessible through the back of the computer. It also completes the 1565 disk drive port. Hopefully someday we’ll be able to make a modern recreation 1565 drive with a plastic case that matches the MEGA65.

KLF is gonna rock you

Here is a visual representation of the waveform of the first few notes of “3 am Eternal” by The KLF, performed by soul singer P. P. Arnold:

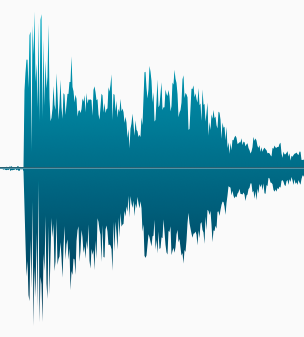
Storing and replicating this waveform exactly as it was performed would require a device and a storage medium that could capture the infinitesimal changes of air pressure in the listener’s ear over time. Digital storage media is neither infinite nor infinitesimal, so we have to make some tradeoffs when digitizing audio. How can we represent this waveform as a collection of numbers, then use those numbers to reproduce an approximation of the waveform on a loudspeaker?

Sample rate

Pulse-code modulation describes the height of a waveform measured periodically, or sampled, over time. We can’t measure every infinitesimal point in time, so we have to choose a sample rate that says how often we take a sample. For audio, a typical sample rate is on the order of kilohertz, or thousands of times per second. A smooth curve in the original waveform is approximated by a stair-step pattern in the digitized waveform.

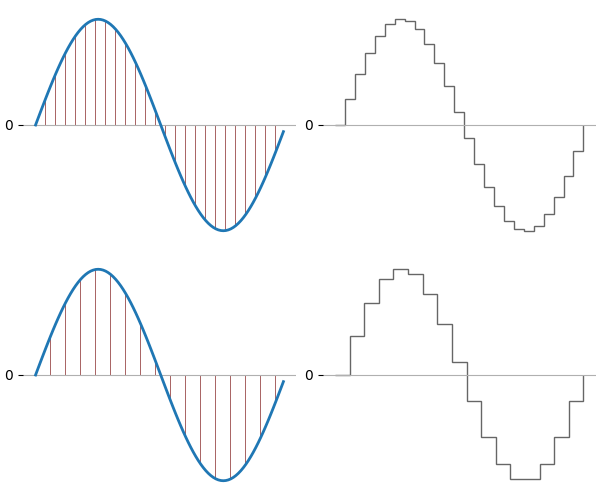
The sample rate for digital audio is a lot like the screen resolution of a digital image. The actual image of an object as seen by the eye could have infinitesimal detail, but to capture it and represent it on a screen, it must be digitized into pixels. The smaller and closer together the pixels, the more detail can be captured and represented. You can think of sample rate as the “horizontal resolution” of the waveform.

Bit depth

We can’t measure the height of each waveform sample infinitesimally either, so this too needs a digital compromise. For example, we could store each sample as 8 bits (one byte) of data. This would give us 256 possible values for the sample. If the measured sample is between two adjacent values, it gets rounded—or quantized—to the closest value. The number of storage bits per sample is the bit depth of the sample (or sample depth). You can think of bit depth as the “vertical resolution” of the waveform.

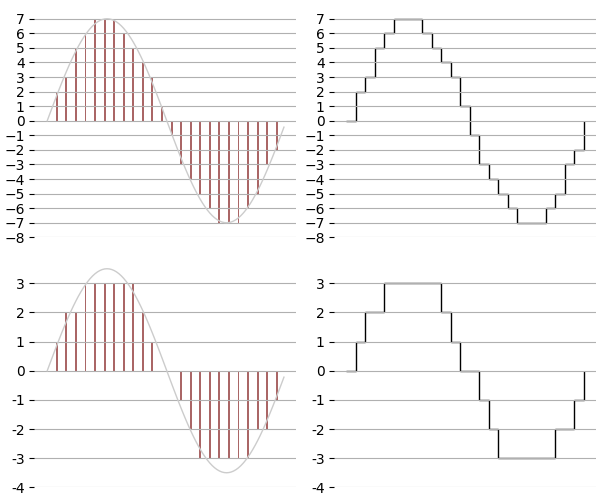
Sample depth can also be understood by analogy with digital images. Each pixel of an image is stored with a digital value that represents its color. The number of possible colors it can use is limited by the bit depth of the color value. Naturally, the more colors the computer can use for a pixel, the more accurately it can represent the original image.

Signed vs. unsigned samples

Conceptually, an audio waveform is a variance in the regular air pressure of a silent room, wiggling positive and negative in a pattern until stabilizing back to zero. You can see the middle line on these waveform diagrams where this level lies. Based on this, waveform samples could be represented as a signed number, with some negative numbers and some positive numbers around a baseline of zero. Or, it could be represented as an unsigned number, where the baseline is the middle value of a range of positive numbers.

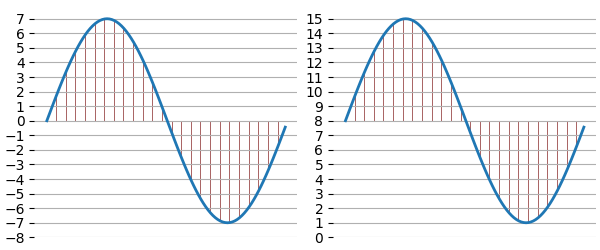
A signed 16-bit sample has a range of -32,768 to +32,767. It is usually stored as a two’s complement value, $8000 (-32,768) up to $FFFF (-1), then $0000 (0) up to $7FFF (32,767). An unsigned 8-bit sample has a range of 0 to 255, where 128 is the baseline of the waveform. It is stored simply as its byte value, $00 (0) to $FF (255). If you’re messing with sample data, you need to know both its bit depth and whether it is signed or unsigned to interpret it correctly.

Size vs. audio quality

Both sample rate and bit depth explain how the amount of data relates to the quality of the reproduction of the original sound. The faster we sample, the more samples we collect, and the more accurate the data is to the original sound. The higher the bit depth of the sample, the more memory is required for each sample, and the more accurate the sample is to the waveform.

Before there were large hard drives, fast Internet transmission speeds, and data compression algorithms tuned for audio, digital music could only be practically distributed on optical fixed-storage compact discs (or “CDs,” as we called them). We purchased these discs at retail establishments with names such as “Tower Records,” and ordered them from printed catalogs to be delivered to our home via postal service from Columbia House at an introductory cost of 10 discs for 1 penny. A typical audio CD stored 74 minutes of uncompressed stereo sound data, using a sample rate of 44.1 kHz and a depth of 16 bits.

We can calculate the amount of sample data on an audio CD with a simple multiplication: 74 minutes x 60 seconds per minute x 44,100 samples per second x 2 bytes per sample x one sample for each stereo channel (2) = 783,216,000 bytes, or almost 747 MiB. Old-timers may remember that a CD-ROM, which uses the same type of disc for storing computer files, has a capacity of 650 MiB. CD-ROMs use the rest of the space for error correction and addressing, so computers can find files and make sure they read them correctly. When an audio CD player reads a sample incorrectly, it just pretends nothing happened and keeps going, so it can use more space for samples.

For perspective, at CD quality, the MEGA65’s 8 megabytes of Attic RAM can contain 45 seconds of audio. As we’ll soon see, we’re actually limited to 64 kilobytes at a time, which would last us 0.35 seconds at 44.1 kHz 16-bit. We’ll need to make some tradeoffs in quality and duration to make practical use of digitized sound.

The following are the durations of 64 kilobytes of sample data at various sample rates and bit depths:

• 4000 Hz, 8-bit: 16.384 seconds
• 4000 Hz, 16-bit: 8.192 seconds
• 8000 Hz, 8-bit: 8.192 seconds
• 8000 Hz, 16-bit: 4.096 seconds
• 11025 Hz, 8-bit: 5.944 seconds
• 11025 Hz, 16-bit: 2.972 seconds
• 16000 Hz, 8-bit: 4.096 seconds
• 16000 Hz, 16-bit: 2.048 seconds

MEGA65 Audio DMAgic

Imagine we had a way to control the speaker membrane directly from a MEGA65 program using a hardware register. What would the program have to do to play back a short digitized sound? The program would write each PCM sample to the register, and it would have to do it at a consistent rate that matches the sample rate. If the sound was digitized at 8 kHz, this program would have to write sample data to the register 8,000 times per second, at even intervals. This is entirely possible with a 40 MHz CPU, but getting the timing right would be a significant programming challenge, especially if the program does other things besides play the sound.

Thankfully, the MEGA65 can help us with this. Reading a series of values from one memory location and writing them to another is the bread and butter of the Direct Memory Access (DMA) chip, a purpose-built chip in the Commodore 65 that the development team called “DMAgic.” DMA is typically used to copy one region of memory to another location very quickly, or fill a region with a value. Normally it does this as quickly as possible. The MEGA65 has enhanced DMAgic with a mechanism for playing audio samples to the DAC at a programmable sample rate, controlled with hardware registers. Your program can even do other things while the sample is playing: playback happens concurrently with program execution.

Because sample timing is managed for us by audio DMA, we don’t need to worry about our program being fast or accurately timed. You can even use audio DMA from BASIC!

Audio DMA specs and techniques

For audio DMA to work its “DMAgic,” a few things must be true:

• The CPU must be running at 40 MHz. (This is the default.)
• Sample data must be in main memory, not Attic RAM.
• Samples must use a bit depth of 16, 8, or 4. Values can be signed or unsigned.
• The playback region cannot exceed 64 KB.

At first glance, this seems a bit limiting, but it’s actually quite powerful with a few tricks. For example, while sample data must be in the first 384 KB of main memory during playback, your program can store its samples in the 8 MB of Attic RAM, then use a DMA copy operation to install it in main memory to be played.

4-bit samples are stored in an interesting way: the DMA must advance through memory by at least one byte per sample, so 4-bit samples use either the top four bits or the bottom four bits of each byte, and you tell audio DMA which bits to use when you play the sound. This means you can have two 4-bit sounds stored in the same bytes, one in the top bits and another in the bottom bits.

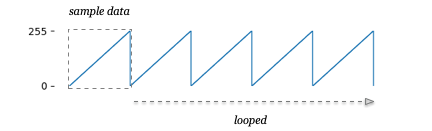
When you play a sound, you can tell audio DMA to stop at the end, or loop back to the beginning automatically and continue playing. Looping is great for short repeating waveforms, or long repeating patterns like drum beats or atmospheric sounds.

With a bit of cleverness, you can play sample data larger than 64 KB by taking advantage of the looping feature. Your program can copy new sample data into the memory region as the sound is being played, so when the playhead loops back to the beginning, it starts playing the new data.

Your program specifies the sample rate to use the play the samples. If you want the samples to sound like the original recording, you play the samples at the rate they were digitized. You can also play the samples at a slower or faster rate to change the pitch and speed of the sample, like spinning a record player at a faster or slower speed. —Oh, uh, records were another way to distribute music before CDs, as analog waveforms etched into grooves on vinyl discs. Sounds were reproduced mechanically by vibrating a needle called a stylus, by running it across the etched groove at a steady speed. Because retro is cool, vinyl album sales have seen a rapid resurgence recently that is expected to grow in 2024, while sales of CDs have dropped in favor of online music streaming.

A synthetic example

Before we figure out how we get recorded sound data into the MEGA65, let’s try out the audio DMA system with some made-up numbers. We’ll use BASIC here, but the procedure is the same in assembly language: we’re just writing to memory and registers. (Try porting this example to assembly language!)

The waveform

To start, let’s draw a simple “sawtooth” waveform into some memory. This will just be the numbers 0 to 255 across 256 bytes of memory, which we will play looped.

10 FOR X=0 TO 255 : POKE $50000+X,X : NEXT X

Channel registers

Each of the four audio DMA channels has 16 bytes of registers. Channel 0’s registers are at addresses $D720 to $D72F, channel 1’s are at $D730 to $D73F, channel 2’s are at $D740 to $D74F, and channel 3’s are at $D750 to $D75F. I’ll refer to each register by its offset $0 through $F. Just know that the registers have the same layout for all four channels.

Switch off channel 0 while we’re setting it up, by writing a 0 to register $0:

20 POKE $D720,0

Enabling the audio DMA system

The audio DMA system must be enabled before it can be used. This is a global setting, address $D711 bit 7:

30 SETBIT $D711,7

Sample addresses

The starting address of the sample is a 24-bit value, across registers $1 to $3. We also want to set the channel 0 playhead, a 24-bit value across registers $A to $C. (Remember, these are all Little Endian.) The starting address is used for looping: when the playhead reaches the end, it’ll jump back to the start address.

40 POKE $D721,$00:POKE $D722,$00:POKE $D723,$05 : REM SAMPLE STARTS AT $5.0000
50 POKE $D72A,$00:POKE $D72B,$00:POKE $D72C,$05 : REM SET PLAYHEAD TO BEGINNING

The end of the sample is stored as a 16-bit value equal to the lower 16 bits of the last address, in registers $7 to $8. In our case, the end address is $5.00FF, so the register value is $00FF.

60 POKE $D727,$FF:POKE $D728,$00

Channel volume

Each audio DMA channel gets two volume settings, with the ability to pan the channel’s output to the Left DAC or the Right DAC in different proportions.

Channels 0 and 1 are considered “left” channels, and channels 2 and 3 are considered “right” channels. The $9 register in each channel’s register bank sets the volume of the signal that it outputs to its device, either the Left DAC or the Right DAC. The register value is between 0 and 255, with 255 being the loudest.

Another set of volume registers allow for each channel to also output to the opposing DAC. Registers $D71C and $D71D set the output of channels 0 and 1, respectively, to the Right DAC. Registers $D71E and $D71F set the output of channels 2 and 3, respectively, to the Left DAC.

This can get a little confusing because the user can subsequently pan the Left DAC or the Right DAC using the Audio & Volume tool in the Freezer, and can even flip the stereo field entirely. If you want to experiment with this, I recommend opening the Freezer tool and setting the “Left Digi” volume up in the left output channel and all the way down in the right output channel, and the “Right Digi” volume down in the left and up in the right, so you can hear clearly through stereo speakers which DAC is being used.

Let’s just set channel 0 to output evenly to both DACs for now. This sawtooth wave is a bit obnoxious, so I’m using a low volume level:

70 POKE $D71C,$22 : POKE $D729,$22

Headphone warning: If you are listening to your MEGA65 with headphones connected directly to the 3.5mm jack, I recommend reducing the master volume in the Audio & Volume tool while you are testing digital audio samples. Incorrect sample data or erroneous register values could cause unexpectedly loud sounds. I prefer to use a set of speakers with an independent volume knob set to a low setting. (Headphones tend not to have their own volume control.)

Sample rate

The sample rate (frequency) is stored as a 24-bit value in registers $4 to $6. This one is a bit weird, but it’ll make sense, I promise.

The value is the 24-bit proportional value of the frequency relative to the CPU speed. For example, if the sample rate is 16 kHz, then the register value is 16 kHz divided by 40 MHz (a ratio), multiplied by 2 to the 24th power minus 1 (the largest 24-bit value). Watch those units when doing the math! The CPU is much faster than the sample rate, so you should get a very small ratio.

Here are the register values for some useful sample rates, pre-calculated for your convenience:

• 4 kHz : 1,662 ($00067E)
• 8 kHz : 3,324 ($000CFC)
• 16 kHz : 6,648 ($0019F8)
• 32 kHz : 13,296 ($0033F0)

For our experiment, we actually want to do something special with the frequency. We have a very short sawtooth waveform, capable of playing a musical note. The middle “A” key on a piano would play this pattern 440 times per second (440 Hz). We have 256 samples, so to achieve a middle A pitch, we need a sample rate of 440 x 256 = 112640 Hz = 112.64 kHz. Proportional to the 40 MHz CPU speed, the 24-bit value is: 47,244 decimal, or $00B88C (that’s “zero zero Baker eight eight Charlie”).

Someone check my math.

80 POKE $D724,$8C:POKE $D725,$B8:POKE $D726,$00 : REM SAMPLE RATE 112.64 KHZ

Sample sign, bit depth, looping, and playback

Finally, we can trigger the sample, with a few last settings in register $0. This register uses the following bits as flags:

• Bit 7: Play it.
• Bit 6: Loop it. We want this to loop our very short sawtooth wave.
• Bit 5: Set this to 0 if the sample value is signed. We’re using unsigned values in this example, so we set this to 1.
• Bits 1-0: The bit depth: 11=16 bits, 10=8 bits (our choice), 01=upper 4 bits, 00=lower 4 bits.

90 POKE $D720, $80 + $40 + $20 + $02
100 GETKEY A$ : REM WAIT FOR A KEYPRESS
110 POKE $D720,0 : REM SWITCH IT OFF! SWITCH IT OFF!

Try it out!

Run this to hear the tone. It’s a bit obnoxious, so press a key to switch it off. If you accidentally press Run/Stop with the sound still playing, use POKE $D720,0 to disable the sound.

You can experiment with different waveforms by writing different values to $5.0000-$5.00FF. Try these:

10 FOR X=0 TO 255 : POKE $50000+X,255*(SGN(X-128)+1) : NEXT X

10 FOR X=0 TO 255 : POKE $50000+X,X-(X-128)*(X>128) : NEXT X

10 FOR X=0 TO 255 : POKE $50000+X,127*SIN(X/255*3.1415)+128 : NEXT X

Converting audio files to raw PCM data

This little experiment to play triangle, sawtooth, and sine waveforms is fun, but not particularly impressive considering that the SID chips can already generate these waveforms on their own. To unleash the true power of audio DMA, we need PCM sample data for more interesting sounds. The MEGA65 does not have a built-in audio digitizer (at least not yet), so we must turn to our trusty modern computers.

There are many ways to record, produce, or otherwise acquire sound files with a modern computer and an Internet connection. Your computer’s operating system probably includes a free sound recording or editing program, and so does your mobile phone. Sound editing software like Audacity is free, and you can also download free sound files from FreeSound.org. Whatever software you’re using, be sure to edit your sound file to trim it to just the length you want your MEGA65 program to play.

Audacity

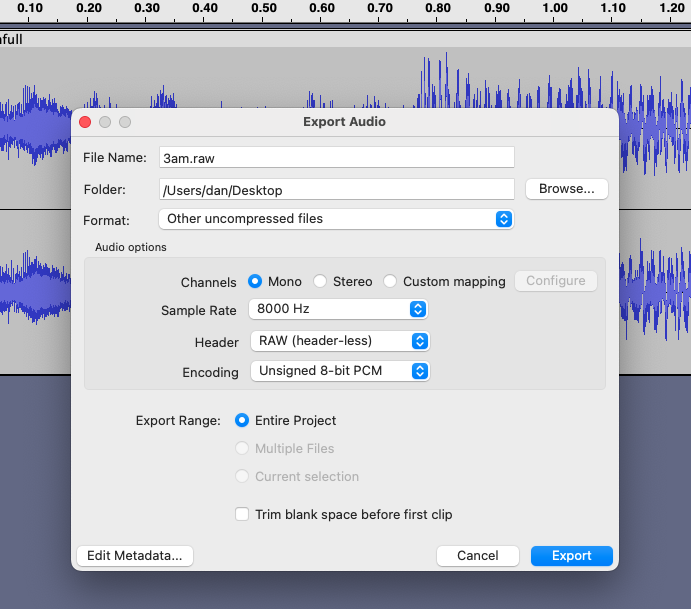
Our goal is to convert the sound file to raw PCM sample data at an appropriate sample rate, and at a bit depth supported by the MEGA65 audio DMA. Audacity can do all of this in a single export step:

1. File menu, Export Audio.
2. Format: “Other uncompressed files”
3. Channels: Mono
4. Sample Rate: 8000 Hz or higher, or select “Other” and enter any rate in Hertz
5. Header: “RAW (header-less)”
6. Encoding: “Signed 16-bit PCM” or “Unsigned 8-bit PCM”
7. Click Export.

Remember that sample rate and bit depth affect data size and sound quality, so choose wisely.

Other modern sound production software may not have all of the same export options. Some of the more expensive software packages on my computer can’t believe I would ever want to export at a sample rate lower than 44.1 kHz. If your software doesn’t export raw PCM sample data, or doesn’t offer the desired sample rate or bit depth, export a .wav file with high quality settings, then use Audacity for the final conversion to raw PCM data with the desired parameters.

It’s important to use the highest quality settings for every processing step until the last one. Because each digital audio file is an approximation of the original waveform, the conversion tool has to use some math to assume the gaps between the samples when converting from one sample rate to another. The more data that goes into that process, the better.

While preparing this Digest, I had occasional issues with Audacity trying to boost the volume of my samples, causing clipping of the signal in some cases that added loud pops to the final sound effect. Notably, this clipping only happened on real hardware and not in Xemu, so be sure to test your samples.

ffmpeg

Audacity is fine, but I like command line tools so I can automate build workflows. The tool for this is ffmpeg, an essential free media conversion tool for video and audio. It’s similar to how we used ImageMagick to convert still images back in a previous Digest. ffmpeg is available for all platforms. On a Mac using Homebrew, install this with: brew install ffmpeg

ffmpeg accepts most audio files as input, including .wav files. Specify the input file with the -i parameter. It’ll detect everything it needs to know about the input data from the file itself.

For the output file, we want something special, so we need to tell it what we want. The -f option selects the bit rate, selected from this list:

• s16le : signed 16-bit Little Endian
• u16le : unsigned 16-bit Little Endian
• u8 : unsigned 8-bit

To convert the file to a different sample rate, use the -ar option, and provide the value in Hertz. To convert a stereo sound to monophonic, specify -ac 1.

ffmpeg -i klf.wav -f u8 -ar 8000 -ac 1 klf.raw

You now have a raw PCM data file. Assuming it’s small enough, you can now copy this to a D81 disk image, and transfer the disk image to your MEGA65. See a previous Digest for more information on how to manage files and disk images.

Playing the digitized sound

The BASIC program above can be modified to play an arbitrary sample file. Replace line 10 with a BLOAD command that loads your sample file to address $50000:

10 BLOAD "KLF.RAW",P($0050000)

You will need to adjust the sample length (line 60) and the sample rate (line 80) as appropriate for your data. You might want to remove the loop flag ($40) from the playback command (line 90). Only include the “unsigned” flag ($20 on line 90) if the sample data is unsigned.

Can you hear the sound, but it’s noisy or crackling? Double-check the “unsigned” bit. Using the unsigned bit when the sample data is signed (and vice versa) will cause transitions from negative to positive values to pop, in a bad way.

What about 4-bit sample data?

None of the audio processing programs I tried offer export of 4-bit samples. How can we make 4-bit samples, to take advantage of this feature of audio DMA?

Compared to something as complex as re-sampling at different sample rates, converting from an unsigned 8-bit sample to an unsigned 4-bit sample is simple. We just lop off the lower four bits, equivalent to dividing by 16. Here’s a simple Python program that does this:

INPUT_FILE = 'klf_8b.raw'
OUTPUT_FILE = 'klf_4b.raw'

data_input = open(INPUT_FILE, 'rb').read()

with open(OUTPUT_FILE, 'wb') as outfile:
  for i in range(len(data_input)):
    samp = int(data_input) // 16
    outfile.write(samp)

This takes the file klf_8b.raw containing unsigned 8-bit samples and produces the file klf_4b.raw containing unsigned 4-bit samples, with each sample in the lower four bits. We can modify our playback program to use this by setting the appropriate flags in the $0 register:

90 POKE $D720, $80 + $20 : REM PLAY IT ONCE, UNSIGNED, 4-BIT LOW

Audio DMA requires that each sample be at separate memory locations, so merely converting a sample from 8-bit to 4-bit doesn’t actually save any space. The space savings comes from storing two 4-bit samples on top of each other, and telling audio DMA to play either the bottom four bits or the top four bits. We can modify this Python script to store two samples together in this way:

INPUT_FILE_ONE = 'klf_8b.raw'
INPUT_FILE_TWO = 'rockyou_8b.raw'
OUTPUT_FILE = 'klf_4b.raw'

data_one = open(INPUT_FILE_ONE, 'rb').read()
data_two = open(INPUT_FILE_TWO, 'rb').read()

# Pad the shorter sample with zeroes, so they are the same length
if len(data_one) < len(data_two):
  data_one += b'\x00' * (len(data_two) - len(data_one))
elif len(data_two) < len(data_one):
  data_two += b'\x00' * (len(data_one) - len(data_two))

with open(OUTPUT_FILE, 'wb') as outfile:
  for i in range(len(data_one)):
    samp_one = int(data_one[i]) // 16
    samp_two = int(data_two[i]) // 16
    result = samp_two * 16 + samp_one
    outfile.write(bytes([result]))

This takes the two 8-bit sample files klf_8b.raw and rockyou_8b.raw, converts them both to 4-bit, then writes them to a single file klf_4b.raw with klf in the lower bits and rockyou in the upper bits.

To tell the playback program which sample to play, set bits 1 and 0 of $D720 accordingly:

90 POKE $D720, $80 + $20 : REM PLAY IT ONCE, UNSIGNED, 4-BIT LOW

90 POKE $D720, $80 + $20 + $01 : REM PLAY IT ONCE, UNSIGNED, 4-BIT HIGH

I have a vivid memory of hearing The KLF’s “3 a.m. Eternal” played on my childhood Amiga 500. Like the MEGA65, the Amiga can play short digitized sounds over four audio DACs. Most Amiga owners didn’t have enough memory to store several minutes of digitized sound, so another kind of music was born. A MOD file encodes music as short digitized sounds played in a pattern of frequencies and timings, saving memory by re-using samples throughout the song. The KLF’s music was largely sample-based and repetitive to begin with, and they even produced some of it on home computers like the Apple II and Atari ST. MOD files can come close to reproducing the original songs within the memory limitations of a vintage computer.

Your MEGA65 includes a MOD player on the Intro Disk, called “Manche,” that uses audio DMA to play sound samples. I found one person’s attempt at a MOD of “3 a.m. Eternal” and was able to play it in Manche on my MEGA65. I can’t say this particular MOD is my favorite remix, but it’s been fun to revive this memory.

Here are a few MOD arrangements of KLF songs for you to enjoy:

• Download: 3ametern.mod
• Download: whattime.mod
• Download: doctorin.mod

Put these in the root of your SD card, then start Intro Disk #1. Open the Music menu, select Manche, and press Return to run the program. Within Manche, press F1, type one of the filenames, then press Return to load the file. Press Space to start playback.

I also made this demonstration disk with the waveform generator program from this issue, as well as a program demonstrating the same sound at different sample rates and bit depths.

• Download: KLF.D81

This Digest is made possible with support from justified ancients, like you! To contribute, visit ko-fi.com/dddaaannn.

See you next month!

— Dan